Giải bài tập trang 32 bài 12 Chia đa thức một biến đã sắp xếp sgk toán 8 tập 1. Câu 71: Không thực hiện phép chia, hãy xét xem đa thức…
Bài 71 trang 32 sgk toán 8 tập 1
Không thực hiện phép chia, hãy xét xem đa thức \(A\) có chia hết cho đa thức \(B\) hay không.
a) \(A = 15{x^4} – 8{x^3} + {x^2}\)
\(B = {1 \over 2}{x^2}\)
b) \(A = {x^2} – 2x + 1\)
\(B = 1 – x\)
Bài giải:
a) \(A,B\) là các đa thức một biến. \(A\) chia \(B\) thì ta lấy từng hạng tử của đa thức \(A\) chia cho đa thức \(B\).
\({x^4},{x^3},{x^2}\) đều chia hết cho \(x^2\)
Do đó \(A\) chia hết cho \(B\)
b) \(A = {x^2} – 2x + 1={(1 – x)^2}\)
Do đó \(A\) chia hết cho \(B\).
Bài 72 trang 32 sgk toán 8 tập 1
Làm tính chia:
\((2{x^4} + {\rm{ }}{x^3}-{\rm{ }}3{x^2} + {\rm{ }}5x{\rm{ }}-{\rm{ }}2){\rm{ }}:{\rm{ }}({x^2}-{\rm{ }}x{\rm{ }} + {\rm{ }}1)\)
Bài giải:
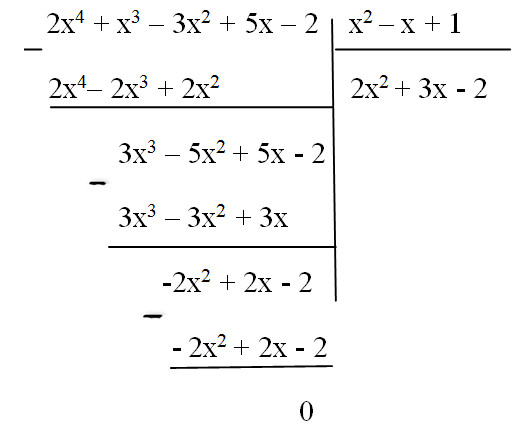
Bài 73 trang 32 sgk toán 8 tập 1
Tính nhanh:
a) \((4{x^2}-{\rm{ }}9{y^2}){\rm{ }}:{\rm{ }}\left( {2x{\rm{ }}-{\rm{ }}3y} \right)\);
b) \((27{x^3}-{\rm{ }}1){\rm{ }}:{\rm{ }}\left( {3x{\rm{ }}-{\rm{ }}1} \right)\);
c) \((8{x^3} + {\rm{ }}1){\rm{ }}:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1)\);
d) \(({x^2}-{\rm{ }}3x{\rm{ }} + {\rm{ }}xy{\rm{ }} – 3y){\rm{ }}:{\rm{ }}\left( {x{\rm{ }} + {\rm{ }}y} \right)\)
Bài giải:
a) \((4{x^2}-{\rm{ }}9{y^2}){\rm{ }}:{\rm{ }}\left( {2x{\rm{ }}-{\rm{ }}3y} \right) \)
\(= \left[ {{{(2x)}^2} – {{(3y)}^2}} \right]:(2x – 3y)\)
\(= (2x – 3y).(2x + 3y):(2x – 3y) = 2x + 3y\);
b) \((27{x^3}-{\rm{ }}1){\rm{ }}:{\rm{ }}\left( {3x{\rm{ }}-{\rm{ }}1} \right) =\left[ {{{(3x)}^3} – {1^3}} \right]:(3x – 1)\)
\(= (3x – 1).\left[ {{{(3x)}^2} + 3x + 1} \right]:(3x – 1) \)
\(= 9{x^2} + 3x + 1\)
c) \((8{x^3} + {\rm{ }}1){\rm{ }}:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1){\rm{ }}\)
\(= \left[ {{{(2x)}^3} + {1^3}} \right]:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1)\)
\(= {\rm{ }}\left( {2x{\rm{ }} + {\rm{ }}1} \right)\left[ {{{(2x)}^2} – 2x + 1} \right]{\rm{ }}:{\rm{ }}(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1)\)
\( = \left( {2x{\rm{ }} + {\rm{ }}1} \right)(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1):(4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1){\rm{ }}\)
\(= {\rm{ }}2x{\rm{ }} + {\rm{ }}1\)
d) \(({x^2}-{\rm{ }}3x{\rm{ }} + {\rm{ }}xy{\rm{ }} – 3y){\rm{ }}:{\rm{ }}\left( {x{\rm{ }} + {\rm{ }}y} \right)\)
\(\eqalign{
& = \left[ {({x^2} + xy) – (3x + 3y)} \right]:(x + y) \cr
& = \left[ {x(x + y) – 3(x + y)} \right]:(x + y) \cr
& = (x + y)(x – 3):(x + y) \cr
& = x – 3 \cr
& \cr} \)
Bài 74 trang 32 sgk toán 8 tập 1
Tìm số \(a\) để đa thức \(2{x^3} – 3{x^2} + x + a\) chia hết cho đa thức \(x + 2\)
Bài giải:
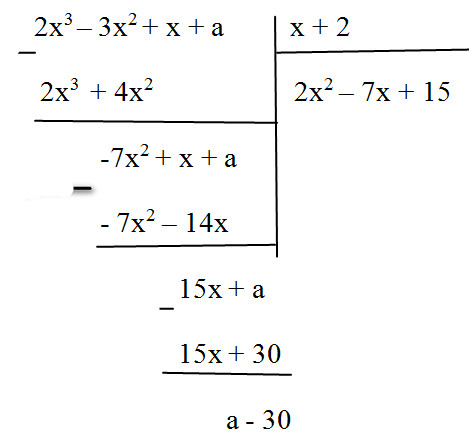
Ta có: \(2{x^3} – 3{x^2} + x + a \)
\(= (2{x^2} – 7x + 15).(x + 2) + a – 30\)
Dư trong phép chia là \((a-30)\) để phép chia là phép chia hết thì dư của phép chia phải bằng \(0\) tức là:
\(a-30=0\Rightarrow a=30\)
Vậy \(a = 30\).
cdnthuathienhue.edu.vn