Giải bài tập trang 31 bài 8 Tính chất của dãy tỉ số bằng nhau Sách giáo khoa (SGK) Toán 7. Câu 61: Tìm hai số x và y, biết rằng…
Bài 62 trang 31 sgk toán 7 tập 1
Tìm hai số x và y, biết rằng: 
và x.y = 10
Lời giải:
Đặt k =
. Ta có x = 2k, y = 5k
Từ xy=10. suy ra 2k.5k = 10 → 10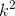 
= 10 → 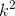= 1 → k = ± 1
Với k = 1 ta được
= 1 suy ra x = 2, y = 5
Với k = -1 ta được
= -1 suy ra x = -2, y = -5
Bài 63 trang 31 sgk toán 7 tập 1
Chứng minh rằng từ tỉ lệ thức \({a \over b} = {c \over d}\,\,(a\, – b \ne 0,\,c\, – d \ne 0)\) ta có thể suy ra tỉ lệ thức \({{a + b} \over {a – b}} = {{c + d} \over {c – d}}\)
Lời giải:
Ta có : \({a \over b} = {c \over d}\,\) suy ra \({a \over c} = {b \over d}\)
Theo tính chất dãy tỉ số bằng nhau ta có
\({a \over c} = {b \over d} = {{a + b} \over {c + d}} = {{a – b} \over {c – d}}\)
Suy ra: \({{a + b} \over {a – b}} = {{c + d} \over {c – d}}\)
Bài 64 trang 31 sgk toán 7 tập 1
Số học sinh bốn khối \(6,7,8,9\) tỉ lệ với các số \(9, 8, 7, 6\). Biết rằng số học sinh khối \(9\) ít hơn số học sinh khối \(7\) là \(70\) học sinh. Tính số học sinh mỗi khối?
Lời giải:
Gọi \(x, y, z, t\) lần lượt là số học sinh các khối \(6, 7, 8, 9\)
Theo đề bài Số học sinh bốn khối \(6,7,8,9\) tỉ lệ với các số \(9, 8, 7, 6\) nên ta có: \({x \over 9} = {y \over 8} = {z \over 7} = {t \over 6}\)
Số học sinh khối \(9\) ít hơn số học sinh khối \(7\) là \(70\) học sinh nên ta có: \(y – t = 70\)
Theo tính chất của dãy tỉ số bằng nhau ta có
\({x \over 9} = {y \over 8} = {z \over 7} = {t \over 6} = {{y – t} \over {8 – 6}} = {{70} \over 2} = 35\)
Do đó:
\(x = 315\)
\(y = 280\)
\(z = 245\)
\(t = 210\)
Trường Cao đẳng nghề Thừa Thiên Huế
