Giải bài tập trang 55 bài 4 đường thẳng song song và đường thẳng cắt nhau SGK Toán 9 tập 1. Câu 24: Cho hai hàm số bậc nhất…
Bài 24 trang 55 sgk Toán 9 tập 1
Bài 24. Cho hai hàm số bậc nhất \(y = 2x + 3k\) và \(y = (2m + 1)x + 2k – 3\).
Tìm điều kiện đối với \(m\) và \(k\) để đồ thị của hai hàm số là:
a) Hai đường thẳng cắt nhau;
b) Hai đường thẳng song song với nhau;
c) Hai đường thằng trùng nhau.
Giải:
Hàm số đã cho là hàm bậc nhất nên \(2m+1\ne 0\Leftrightarrow m\ne -{1\over 2}\)
a) Hai đường thẳng cắt nhau:
\(\Leftrightarrow 2\neq 2m+1\)
\(\Leftrightarrow m\neq \frac{1}{2}\)
Kết hợp điều kiện hàm bậc nhất \(m \ne \pm {1 \over 2}\)
b) Hai đường thẳng song song:
\(\Leftrightarrow \left\{\begin{matrix} 2=2m+1\\ 3k\neq 2k-3 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m=\frac{1}{2}\\ k\neq -3 \end{matrix}\right.\)
c) Hai đường thẳng trùng nhau:
\(\Leftrightarrow \left\{\begin{matrix} 2=2m+1\\ 3k= 2k-3 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m=\frac{1}{2}\\ k= -3 \end{matrix}\right.\)
Bài 25 trang 55 sgk Toán 9 tập 1
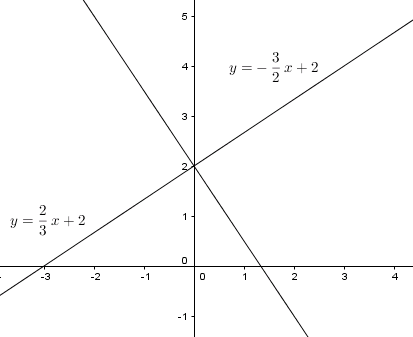
a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
\(y = {2 \over 3}x + 2\); \(y = – {3 \over 2}x + 2\)
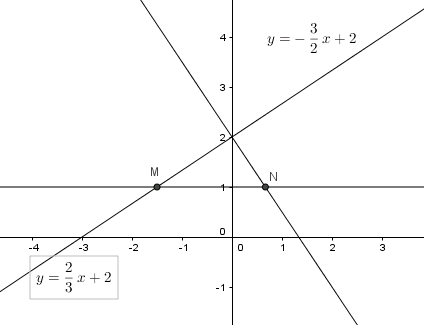
b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại điểm có tung độ bằng 1, cắt các đường thẳng \(y = {2 \over 3}x + 2\) và \(y = – {3 \over 2}x + 2\) theo thứ tự tại hai điểm M và N. Tìm tọa độ của hai điểm M và N.
Giải:
a) Đồ thị được vẽ như hình dưới
b)
Vì M thuộc đồ thị \(y=1\) và \(y = \frac{2}{3}x + 2\)
\(\Rightarrow \frac{2}{3}x_M+2=1\Rightarrow x_M=\frac{-3}{2}\)
\(\Rightarrow M\left ( -\frac{3}{2};1 \right )\)
Vì N thuộc đồ thị \(y=1\) và \(y = – \frac{3}{2}x + 2\)
\(\Rightarrow -\frac{3}{2}x_N+2=1\Rightarrow x_N=\frac{2}{3}\)
\(\Rightarrow N\left ( \frac{2}{3};1 \right )\)
Ta có đồ thị:
Bài 26 trang 55 sgk Toán 9 tập 1
Bài 26. Cho hàm số bậc nhất \(y = ax – 4\) (1). Hãy xác định hệ số \(a\) trong mỗi trường hợp sau:
a) Đồ thị của hàm số (1) cắt đường thẳng \(y = 2x – 1\) tại điểm có hoành độ bằng \(2\).
b) Đồ thị của hàm số (1) cắt đường thẳng \(y = -3x + 2\) tại điểm có tung độ bằng \(5\).
Giải:
a) Giả sử hai hàm số cắt nhau tại \(A(x_A;y_A)\), hoành độ giao điểm là \(x_A=2\), \(A\) là giao điểm nên tọa độ \(A\) thỏa mãn phương trình hàm số \(y = 2x – 1\) do đó ta có:
\(y_A =2.2-1=3\Rightarrow A(2;3)\)
Thay tọa độ điểm \(A\) vào phương trình (1) ta được:
\(3=a.2-4\Rightarrow a=\frac{7}{2}\)
b) Giả sử hai hàm số cắt nhau tại \(B(x_B;y_B)\), tung độ điểm cắt phương trình (1) là \(y_B=5\), \(B\) là giao điểm nên tọa độ của \(B\) thỏa mãn phương trình hàm số \(y = -3x + 2\) do đó ta có:
\(5=-3.x_B+2\Rightarrow x_B=-1\Rightarrow B(-1;5)\)
Thay tọa độ điểm \(B\) vào phương trình (1):
\(5=-1.a-4\Rightarrow a=-9\)
cdnthuathienhue.edu.vn