Giải bài tập trang 86, 87 bài 6 đối xứng trục Sách bài tập (SBT) Toán 8 tập 1. Câu 60: Chứng minh rằng AD = AE…
Câu 60 trang 86 Sách bài tập(SBT) Toán 8 tập 1
Cho tam giác ABC có\(\widehat A = {70^0}\), điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC.
a. Chứng minh rằng AD = AE
b. Tính số đo góc DAE.
Giải:
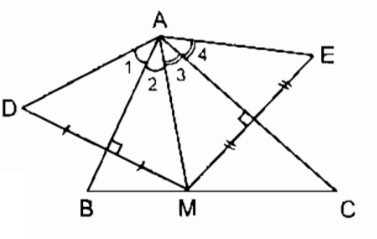
a. Vì D đối xứng với M qua trục AB
⇒ AB là đường trung trực MD.
⇒ AD = AM (tính chất đường trung trực) (1)
⇒ Vì E đối xứng với M qua trục AC
⇒ AC là đường trung trực của ME
⇒ AM = AE ( tính chất đường trung trực) (2)
⇒ Từ (1) và (2) suy ra : AD = AE
b. AD = AM suy ra ∆ AMD cân tại A có AB ⊥ MD
nên AB cũng là đường phân giác của góc MAD
\( \Rightarrow {\widehat A_1} = {\widehat A_2}\)
AM = AE suy ra ∆ AME cân tại A có AC ⊥ ME nên AC cũng là đường phân giác của \(\widehat {MAE}\)
\( \Rightarrow {\widehat A_3} = {\widehat A_4}\)
\(\widehat {DAE} = {\widehat A_1} + {\widehat A_2} + {\widehat A_3} + {\widehat A_4}\)
\(= 2\left( {{{\widehat A}_2} + {{\widehat A}_3}} \right) = 2\widehat {BAC} = {2.70^0} = {140^0}\)
Câu 61 trang 87 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác nhọn ABC có\(\widehat A = {60^0}\), trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a. Chứng minh ∆ BHC = ∆ BMC.
b. Tính \(\widehat {BMC}\)
Giải:
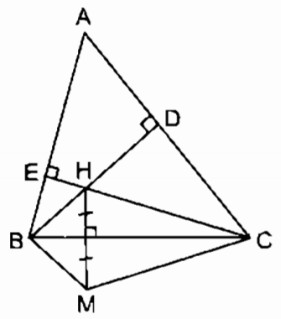
a. Vì M đối xứng với H qua trục BC
⇒ BC là đường trung trực của HM
⇒ BH = BM ( tính chất đường trung trực)
CH = CM ( tính chất đường trung trực)
Suy ra: ∆ BHC = ∆ BMC (c.c.c)
b. Gọi giao điểm BH với AC là D, giao điểm của CH và AB là E
H là trực tâm của ∆ ABC
⇒ BD ⊥ AC, CE ⊥ AB
Xét tứ giác ADHE ta có:
\(\widehat {DHE} = {360^0} – \left( {\widehat A + \widehat D + \widehat E} \right) \)
\(= {360^0} – \left( {{{60}^0} + {{90}^0} + {{90}^0}} \right) = {120^0}\)
\(\widehat {BHC} = \widehat {DHE}\) (đối đỉnh)
∆ BHC = ∆ BMC (chứng minh trên)
\( \Rightarrow \widehat {BMC} = \widehat {BHC}\)
Suy ra: \(\widehat {BMC} = \widehat {DHE} = {120^0}\)
Câu 62 trang 87 Sách bài tập (SBT) Toán 8 tập 1
Cho hình thang vuông ABCD\(\left( {\widehat A = \widehat D = {{90}^0}} \right)\). Gọi điểm H la điểm đối xứng với B qua AD, I là giao điểm của CH và AD. Chứng minh rằng \(\widehat {AIB} = \widehat {DIC}\)
Giải:
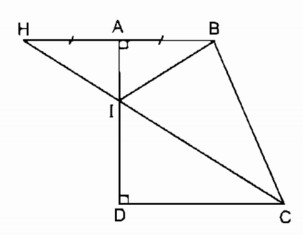
B và H đối xứng qua AD.
I và A đối xứng với chính nó qua AD
Nên \(\widehat {AIB}\) đối xứng với \(\widehat {AIH}\) qua AD
\( \Rightarrow \widehat {AIB} = \widehat {AIH}\)
\(\widehat {AIH} = \widehat {DIC}\)( đối đỉnh)
Suy ra: \(\widehat {AIB} = \widehat {DIC}\)
Câu 63 trang 87 Sách bài tập (SBT) Toán 8 tập 1
Cho hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy (AB không vuông góc với xy). Gọi A’ là điểm đối xứng với A qua xy, C là giao điểm của A’B và xy. Gọi M là điểm bất kì khác C thuộc đường thẳng xy. Chứng minh rằng AC + CB
Giải:
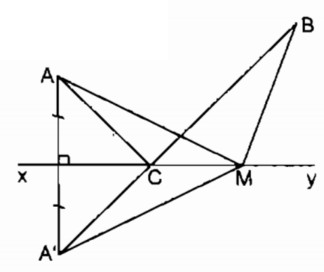
Vì A’ đối xứng với A qua xy
⇒ xy là đường trung trực của AA’
⇒ CA’ = CA (tính chất đường trung trực)
MA = MA’ (tính chất đường trung trực)
AC + CB = A’C + CB = A’B (1)
MA + MB = MA’ + MB (2)
Trong ∆ MA’B ta có:
A’B
Từ (1), (2) và (3) suy ra: AC + CB
cdnthuathienhue.edu.vn