Giải bài tập trang 13 bài 12 chia đa thức một biến đã sắp xếp Sách bài tập (SBT) Toán 8 tập 1. Câu 48: Làm tính chia…
Câu 48 trang 13 Sách bài tập (SBT) Toán 8 tập 1
Làm tính chia:
a. \(\left( {6{x^2} + 13x – 5} \right):\left( {2x + 5} \right)\)
b. \(\left( {{x^3} – 3{x^2} + x – 3} \right):\left( {x – 3} \right)\)
c. \(\left( {2{x^4} + {x^3} – 5{x^2} – 3x – 3} \right):\left( {{x^2} – 3} \right)\)
Giải:
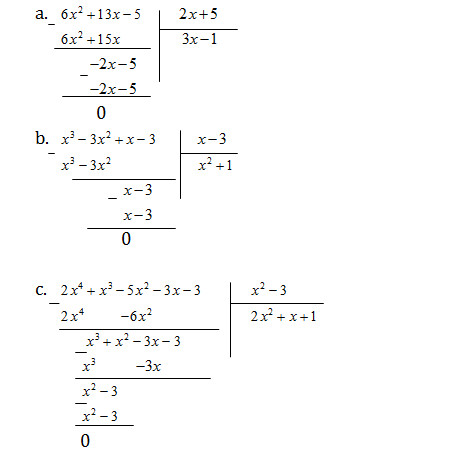
Câu 49 trang 13 Sách bài tập(SBT) Toán 8 tập 1
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
a. \(\left( {12{x^2} – 14x + 3 – 6{x^3} + {x^4}} \right):\left( {1 – 4x + {x^2}} \right)\)
b. \(\left( {{x^5} – {x^2} – 3{x^4} + 3x + 5{x^3} – 5} \right):\left( {5 + {x^2} – 3x} \right)\)
c. \(\left( {2{x^2} – 5{x^3} + 2x + 2{x^4} – 1} \right):\left( {{x^2} – x – 1} \right)\)
Giải:
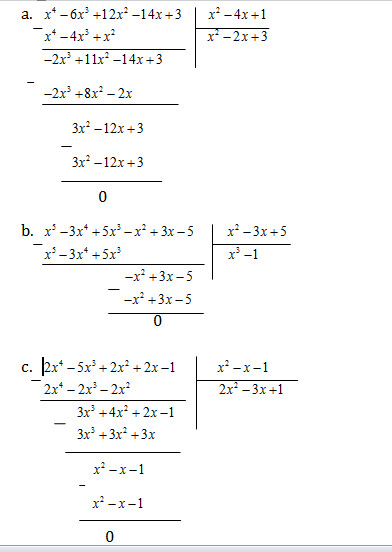
Câu 50 trang 13 Sách bài tập (SBT) Toán 8 tập 1
Cho hai đa thức
A=\({x^4} – 2{x^3} + {x^2} + 13x – 11\) và B=\({x^2} – 2x + 3\)
Tìm thương Q và dư R sao cho A= B.Q + R.
Giải:
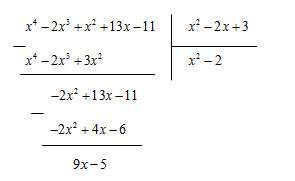
Ta có thương Q= và dư R= \(9x – 5\)
\({x^4} – 2{x^3} + {x^2} + 13x – 11\)= \(({x^2} – 2x + 3)\left( {{x^2} – 2} \right) + \left( {9x – 5} \right)\)
Câu 51 trang 13 Sách bài tập (SBT) Toán 8 tập 1
Tìm a sao cho đa thức
\({x^4} – {x^3} + 6{x^2} – x + a\) chia hết cho đa thức \({x^2} – x + 5\)
Giải:
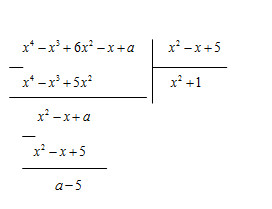
Để có phép chia hết thì số dư bằng 0 \( \Rightarrow a – 5 = 0 \Rightarrow a = 5\)
cdnthuathienhue.edu.vn