Giải bài tập trang 121 bài ôn tập chương I – hệ thức lượng trong tam giác vuông Sách bài tập (SBT) Toán 9 tập 1. Câu 88: Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B…
Câu 88 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1
Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc “nâng” để nhìn thấy máy bay tại vị trí A là $40^\circ $ và tại vị trí B là $30^\circ $ (h.34). Hãy tìm độ cao của máy bay.
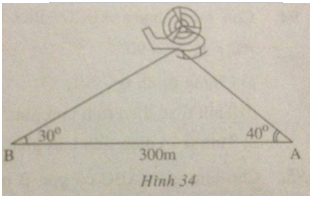
Gợi ý làm bài
Gọi C là vị trí của máy bay.
Kẻ \(CH \bot AB\)
Trong tam giác vuông ACH, ta có:
\(AH = CH.\cot g\widehat A\,(1)\)
Trong tam giác vuông BCH, ta có:
\(BH = CH.\cot g\widehat B\,(2)\)
Từ (1) và (2) suy ra:
\((AH + BH) = CH.\cot g\widehat A + CH.\cot g\widehat B\)
Suy ra:
\(\eqalign{
& CH = {{AB} \over {\cot g\widehat A + \cot g\widehat B}} \cr
& = {{AB} \over {\cot g40^\circ + \cot g30^\circ }} \approx 102,606\,(cm) \cr} \)
Câu 89 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hình thang với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm, góc tù bằng \(120^\circ \). Tính chu vi và diện tích của hình thang đó.
Gợi ý làm bài
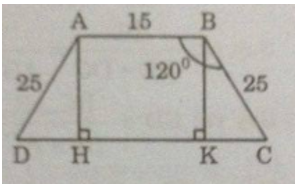
Giả sử hình thang ABCD có đáy nhỏ AB = 15cm, cạnh bên AD = BC =25cm, \(\widehat {ABC} = \widehat {BAD} = 120^\circ \).
Kẻ \(AH \bot CD,BK \bot CD\)
Vì ABKH là hình chữ nhật nên:
AB = KH =15 (cm)
Ta có:
\(\widehat {ADC} + \widehat {DAB} = 180^\circ \)
Suy ra:
\(\widehat {ADC} = 180^\circ – \widehat {DAB} = 180^\circ – 120^\circ = 60^\circ \)
Trong tam giác vuông ADH, ta có:
\(\eqalign{
& DH = AD.\cos \widehat {ADC} \cr
& = 25.\cos 60^\circ = 12,5\,(cm) \cr} \)
\(\eqalign{
& AH = AD.\sin \widehat {ADC} \cr
& = 25.\sin 60^\circ = {{25\sqrt 3 } \over 2}\,)\,\,(cm) \cr} \)
Mà ∆ADH=∆BCK (cạnh huyền, cạnh góc vuông)
Suy ra: DH = CK = 12,5 (cm)
Chu vi hình thang ABCD là:
AB + BC + CD + DA = AB + BC + (CK + KH + HD) + DA
= 15 + 25 + (12,5 + 15 + 12,5) + 25 = 105 (cm)
Chu vi hình thang ABCD là:
\(\eqalign{
& {S_{ABCD}} = {{AB + CD} \over 2}.AH \cr
& = {{15 + 40} \over 2}.{{25\sqrt 2 } \over 2} \approx 595,392\,\,\left( {c{m^2}} \right) \cr} \)
Câu 90 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm.
a) Tính \(BC,\widehat B,\widehat C\);
b) Phân giác của góc A cắt BC tại D. Tính BD, CD.
c) Từ D kẻ DE và DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích của tứ giác AEDF.
Gợi ý làm bài
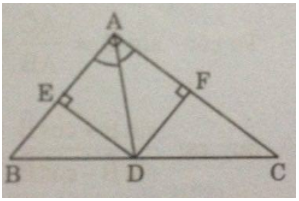
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC,ta có.
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} \cr
& = 36 + 64 = 100\,(cm) \cr} \)
Suy ra: \(BC = \sqrt {100} = 10\,(cm)\)
Ta có: \(\sin C = {{AB} \over {AC}} = {6 \over {10}} = 0,6\)
Suy ra: \(\widehat C = 36^\circ 52’\)
Ta có: \(\widehat B + \widehat C = 90^\circ \)
\( \Rightarrow \widehat B = 90^\circ – \widehat C = 90^\circ – 36^\circ 52′ = 53^\circ 8’\)
b) Ta có:
\({{BD} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác)
Suy ra: \({{BD} \over {BD + DC}} = {{AB} \over {AB + AC}}\)
Suy ra: \(BD = {{BC.AB} \over {BC}} = {{{{40} \over 7}.6} \over {10}} = {{24} \over 7}\,(cm)\)
Chu vi tứ giác AEDF bằng: \(4AE = 4.{{24} \over 7} = {{96} \over 7}\,(cm)\)
Diện tích tứ giác AEDF bằng: \(A{E^2} = {\left( {{{24} \over 7}} \right)^2} = {{576} \over {49}}\,\left( {c{m^2}} \right)\)
Câu 91 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a.
a) Tính \({{\sin B + c{\rm{osB}}} \over {\sin B – c{\rm{osB}}}}.\)
b) Tính chiều cao của hình thang ABCD.
Gợi ý làm bài
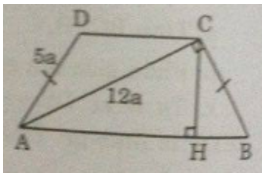
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(A{B^2} = B{C^2} + A{C^2} = {(5a)^2} + {(12a)^2} = 169{a^2}\)
Suy ra: \(AB = \sqrt {169{a^2}} = 13a\)
Ta có: \(\sin \widehat B = {{AC} \over {AB}} = {{12a} \over {13a}} = {{12} \over {13}}\)
\(\cos \widehat B = {{BC} \over {AB}} = {{5a} \over {13a}} = {5 \over {13}}\)
Suy ra:
\({{\sin \widehat B + \cos \widehat B} \over {\sin \widehat B – \cos \widehat B}} = {{{{12} \over {13}} + {5 \over {13}}} \over {{{12} \over {13}} – {5 \over {13}}}} = {{{{17} \over {13}}} \over {{7 \over {13}}}} = {{17} \over {13}}.{{13} \over 7} = {{17} \over 7}\)
b) Kẻ \(CH \bot AB\)
Trong tam giác vuông BCH, ta có:
\(CH = CB.\sin \widehat B = 5a.{{12} \over {13}} = {{60a} \over {13}}\)
cdnthuathienhue.edu.vn