Giải bài tập trang 112 bài 3 bảng lượng giác Sách bài tập (SBT) Toán 9 tập 1. Câu 47: Cho x là một góc nhọn, biểu thức sau đây có giá trị âm hay dương? Vì sao?…
Câu 47. Trang 112 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho x là một góc nhọn, biểu thức sau đây có giá trị âm hay dương? Vì sao?
a) \(tg28^\circ \) và \(\sin 28^\circ \); b) \(\cot g42^\circ \) và \(\cos 42^\circ \);
c) \(\cot g73^\circ \) và \(\sin 17^\circ \); d) \(tg32^\circ \) và \(\cos 58^\circ \).
Gợi ý làm bài:
a) Ta có: \(0^\circ
b) Ta có: \(0^\circ 0\)
c) Ta có:
* Nếu x = 45° thì sinx =cosx, suy ra: \({\mathop{\rm s}\nolimits} {\rm{inx}} – \cos x = 0\)
* Nếu x
Vì x 45^\circ \), suy ra: \({\mathop{\rm s}\nolimits} {\rm{inx}}
Vậy \({\mathop{\rm s}\nolimits} {\rm{inx}} – \cos x
* Nếu x > 45° thì \(\cos x = \sin (90^\circ – x)\)
Vì x > 45° nên \(90^\circ – x \sin (90^\circ – x)\)
Vậy \({\mathop{\rm s}\nolimits} {\rm{inx}} – c{\rm{osx > 0}}\).
d) Ta có:
* Nếu x = 45° thì tgx = cotgx, suy ra: tgx = cotgx = 0
* Nếu x
Vì x > 45° nên \(90^\circ – x tg(90^\circ – x)\)
Vậy tgx – cotgx >0.
Câu 48. Trang 112 Sách Bài Tập (SBT) Toán 9 Tập 1
a. \(tg28^\circ \) và sin28° b. cotg42° và cos42°
c. cotg73° và sin17° d. tg32° và cos58°
Gợi ý làm bài:
a) \(tg28^\circ = {{\sin 28^\circ } \over {\cos 28^\circ }} = \sin 28^\circ .{1 \over {\cos 28^\circ }}\) (1)
Vì 0 1 \Rightarrow \sin 28^\circ .{1 \over {\cos 28^\circ }} > \sin 28^\circ \) (2)
Từ (1) và (2) suy ra: tg28° > sin28°
b) Ta có: \(\cot g42^\circ = {{\cos 42^\circ } \over {\sin 42^\circ }} = c{\rm{os42}}^\circ .{1 \over {\sin 42^\circ }}\) (1)
Vì 0 1 \Rightarrow \cos 42^\circ .{1 \over {\sin 42^\circ }} > \cos 42^\circ \) (2)
Từ (1) và (2) suy ra: cotg42° > cos42°
c) Ta có: 17° +73° =90° (1)
\(\cot g73^\circ = {{\cos 73^\circ } \over {\sin 73^\circ }} = \cos 73^\circ .{1 \over {\sin 73^\circ }}\) (2)
Vì 0
Từ (1), (2) và (3) suy ra: cotg73° > sin17°
d) Ta có: 32° +58° = 90° (1)
\(tg32^\circ = {{\sin 32^\circ } \over {\cos 32^\circ }} = \sin 32^\circ .{1 \over {\cos 32^\circ }}\) (2)
Vì 0 1 \Rightarrow \sin 32^\circ .{1 \over {{\rm{cos32}}^\circ }} > \sin 32^\circ \) (3)
Từ (1), (2) và (3) suy ra: tg32° > cos58°
Câu 49. Trang 112 Sách Bài Tập (SBT) Toán 9 Tập 1
Tam giác ABC vuông tại A, có \(AC = {1 \over 2}BC\). Tính :
\(\sin B,\cos B,tgB,\cot gB.\)
Gợi ý làm bài:
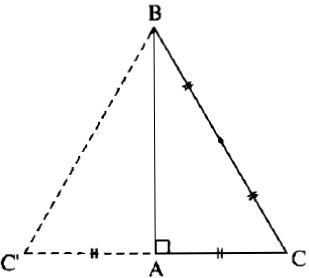
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
\(\eqalign{
& \Rightarrow A{B^2} = B{C^2} – A{C^2} \cr
& = B{C^2} – {{B{C^2}} \over 4} = {{3B{C^2}} \over 4} \cr
& \Rightarrow AB = {{BC\sqrt 3 } \over 2} \cr} \)
Vậy: \(\sin \widehat B = {{AC} \over {BC}} = {{{1 \over 2}BC} \over {BC}} = {1 \over 2}\)
\({\rm{cos}}\widehat B = {{AB} \over {BC}} = {{{{\sqrt 3 } \over 2}BC} \over {BC}} = {{\sqrt 3 } \over 2}\)
\(tg\widehat B = {{AC} \over {AB}} = {{{1 \over 2}BC} \over {{{\sqrt 3 } \over 2}BC}} = {{\sqrt 3 } \over 3}\)
\(\cot g\widehat B = {1 \over {tgB}} = {1 \over {{{\sqrt 3 } \over 3}}} = \sqrt 3 \)
cdnthuathienhue.edu.vn