Giải bài tập trang 95, 96 bài 8 Đối xứng tâm sgk toán 8 tập 1. Câu 50: Vẽ điểm A’ đối xứng với A qua B, vẽ điểm C đối xứng với C qua B (h.81)…
Bài 50 trang 95 sgk toán 8 tập 1
Vẽ điểm A’ đối xứng với A qua B, vẽ điểm C đối xứng với C qua B (h.81).
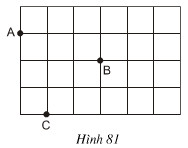
Bài giải:
Xem hình vẽ.
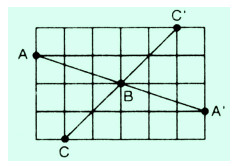
Bài 51 trang 96 sgk toán 8 tập 1
Trong mặt phẳng tọa độ, cho điểm \(H\) có tọa độ \((3; 2)\). Hãy vẽ điểm \(K\) đối xứng với \(H\) qua gốc tọa độ và tìm tọa độ \(K\).
Bài giải:
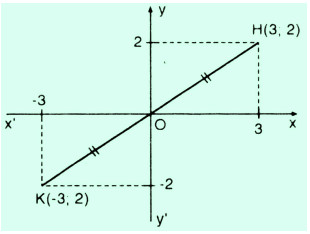
Trên mặt phẳng tọa độ \(xOy\), xác định điểm \(H\) có tọa độ \((3 ; 2)\). Như vậy ta đã có hai điểm \(O\) và \(H\). Để vẽ điểm \(K\) đối xứng với điểm \(H\) qua gốc tọa độ, ta vẽ một đường thẳng đi qua hai điểm \(O\) và \(H\), rồi lấy điểm \(K\) thuộc \(OH\) sao cho \(O\) là trung điểm của đoạn \(KH\). Dựng các đường thẳng song song với trục \(Ox\) và trục \(Oy\) ta tìm đk tọa độ \(K\)
Khi đó điểm \(K\) có tọa độ \((-3 ; -2)\).
Bài 52 trang 96 sgk toán 8 tập 1
Cho hình bình hành \(ABCD\). Gọi \(E\) là điểm đối xứng với \(D\) qua điểm \(A\), gọi \(F\) là điểm đối xứng với \(D\) qua điểm \(C\). Chứng minh rằng điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\).
Bài giải:
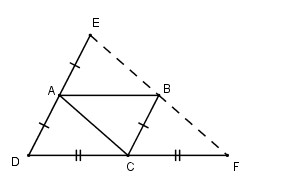
\(AE // BC\) (vì \(AD // BC\))
\(AE = BC\) (cùng bằng \(AD\))
nên \(ACBE\) là hình bình hành theo dấu hiệu nhận biết hình bình hành.
Suy ra: \(BE // AC, BE = AC\) (1)
Tương tự \(BF // AC, BF = AC\) (2)
\(BE\) và \(BF\) cùng song song với \(AC\) và cùng đi qua điểm \(B\) nên theo tiên đề Ơ -clit \(BE\) trùng \(BF\), hay \(B,E,F\) thẳng hàng.
Từ (1) và (2) \( BE = BF\) do đó \(B\) là trung điểm của \(EF\).
Vậy \(E\) đối xứng với \(F\) qua \(B\).
Bài 53 trang 96 sgk toán 8 tập 1
Cho hình 82, trong đó \(MD // AB\) và \(ME // AC\). Chứng minh rằng điểm \(A\) đối xứng với điểm \(M\) qua \(I\).
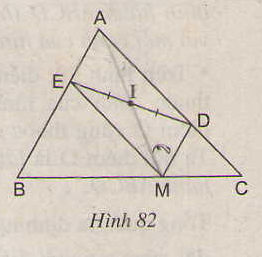
Bài giải:
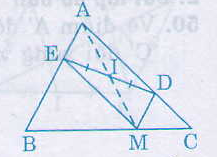
Ta có \(MD // AE\) (vì \(MD // AB\))
\(ME // AD\) (vì \(ME // AC\))
Do đó \(AEMD\) là hình bình hành theo định nghĩa hình bình hành, \(I\) là trung điểm của \(DE\) nên \(I\) là giao điểm của hai đường chéo \(DE\) và \(AM\) và \(I\) cũng là trung điểm của \(AM\) (theo tính chất hình bình hành).
Do đó \(A\) đối xứng với \(M\) qua \(I\).
cdnthuathienhue.edu.vn