Giải bài 6, 7, 8, 9 trang 61, 62 SBT Toán 9 tập 1

Giải bài tập trang 61, 62 bài 2 hàm số bậc nhất Sách bài tập (SBT) Toán 9 tập 1. Câu 6: Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b xét xem hàm số nào nghịch biến…

Câu 6 trang 61 Sách Bài Tập (SBT) Toán 9 Tập 1

Trong  các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b xét xem  hàm số nào nghịch biến?

a) \(y = 3 – 0,5x\);                                 b) \(y =  – 1,5x\);                

c) \(y = 5 – 2{x^2}\)                                    d) \(y = \left( {\sqrt 2  – 1} \right)x + 1\)

e) \(y = \sqrt 3 \left( {x – \sqrt 2 } \right)\)                        f) \(y + \sqrt 2  = x – \sqrt 3 \)

Gợi ý làm bài:

a) Ta có: \(y = 3 – 0,5x =  – 0,5x + 3\) là hàm số bậc nhất

Hệ số \(a =  – 0,5\), hệ số \(b = 3\)

Vì \( – 0,5

b) Ta có: \(y =  – 1,5x\) là hàm số bậc nhất

Hệ số \(a =  – 1,5\), hệ số \(b = 0\)

Vì \( – 1,5

c) Ta có: \(y = 5 – 2{x^2}\) không phải là hàm số bậc nhất.

d) Ta có: \(y = \left( {\sqrt 2  – 1} \right)x + 1\) là hàm số bậc nhất

Hệ số \(a = \sqrt 2  – 1\), hệ số \(b = 1\)

Vì \(\sqrt 2  – 1 > 0\) nên hàm số đồng biến.

e) Ta có: \(y = \sqrt 3 \left( {x – \sqrt 2 } \right) = \sqrt {3x}  – \sqrt 6 \) là hàm số bậc nhất

Hệ số \(a = \sqrt 3 \), hệ số \(b = \sqrt 6 \)

Vì \(\sqrt 3  > 0\) nên hàm số đồng biến.

f) Ta có: \(y + \sqrt 2  = x – \sqrt 3  \Rightarrow y = x – \sqrt 3  – \sqrt 2 \) là hàm số bậc nhất

Hệ số \(a = 1,b =  – \sqrt 3  – \sqrt 2 \)

Vì 1 > 0 nên hàm số đồng biến.

Câu 7 trang 62 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho hàm số bậc nhất \(y = \left( {m + 1} \right)x + 5.\)

a)      Tìm giá trị của m để hàm số y là hàm số đồng biến;

b)      Tìm giá trị của m để hàm số y là hàm số nghịch biến.

Gợi ý làm bài:

a) Hàm số đồng biến khi \(a = m + 1 > 0 \Leftrightarrow m >  – 1\).

b) Hàm số nghịch biến khi \(a = m + 1

Câu 8 trang 62 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho hàm số \(y = \left( {m + 1} \right)x + 5\).

a)      Hàm số là đồng biến hay nghịch biến trên R ? vì sao?

b)      Tính các giá trị tương ứng của y khi x nhận các giá trị sau:

0;              1;               \(\sqrt 2 \);                \(3 + \sqrt 2 \);                \(3 – \sqrt 2 \).

c)      Tính các giá trị tương ứng của x khi y nhận các giá trị sau:

0;               1;               8;                 \(2 + \sqrt 2 \);               \(2 – \sqrt 2 \).

Gợi ý làm bài:

Hàm số \(y = \left( {3 – \sqrt 2 } \right)x + 1\) có hệ số \(a = 3 – \sqrt 2 \), hệ số \(b = 1\) .

a) Ta có:  nên hàm số đồng biến trên R

b) Các giá trị của y được thể hiện trong bảng sau:

c) Các giá trị tương ứng của x:

Với  y = 0

\(\eqalign{
& y = 0 \Leftrightarrow \left( {3 – \sqrt 2 } \right)x + 1 = 0 \cr 
& \Leftrightarrow \left( {3 – \sqrt 2 } \right)x = – 1 \cr 
& \Leftrightarrow x = {{ – 1} \over {3 – \sqrt 2 }} \cr 
& \Leftrightarrow x = {{ – 1\left( {3 + \sqrt 2 } \right)} \over {\left( {3 – \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& \Leftrightarrow x = {{ – \left( {3 + \sqrt 2 } \right)} \over 7} \cr} \)

Với y = 1

\(\eqalign{
& y = 1 \Leftrightarrow \left( {3 – \sqrt 2 } \right)x + 1 = 1 \cr 
& \Leftrightarrow \left( {3 – \sqrt 2 } \right)x = 0 \Leftrightarrow x = 0 \cr} \)

Với y = 8

\(\eqalign{
& y = 8 \Leftrightarrow \left( {3 – \sqrt 2 } \right)x + 1 = 8 \cr 
& \Leftrightarrow \left( {3 – \sqrt 2 } \right)x = 7 \cr 
& \Leftrightarrow x = {7 \over {3 – \sqrt 2 }} \cr 
& \Leftrightarrow x = {{7\left( {3 + \sqrt 2 } \right)} \over {\left( {3 – \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& \Leftrightarrow x = {{7\left( {3 + \sqrt 2 } \right)} \over 7} = 3 + \sqrt 2 \cr} \)

Với \(y = 2 + \sqrt 2 \)

\(\eqalign{
& \Leftrightarrow \left( {3 – \sqrt 2 } \right)x + 1 = 2 + \sqrt 2 \cr 
& \Leftrightarrow \left( {3 – \sqrt 2 } \right)x = 1 + \sqrt 2 \cr 
& \Leftrightarrow x = {{1 + \sqrt 2 } \over {3 – \sqrt 2 }} = {{\left( {1 + \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)} \over {\left( {3 – \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& = {{3 + \sqrt 2 + 3\sqrt 2 + 2} \over {9 – 2}} = {{5 + 4\sqrt 2 } \over 7} \cr} \)

Với \(y = 2 – \sqrt 2 \)

\(\eqalign{
& \Leftrightarrow \left( {3 – \sqrt 2 } \right)x + 1 = 2 – \sqrt 2 \cr 
& \Leftrightarrow \left( {3 – \sqrt 2 } \right)x = 1 – \sqrt 2 \cr 
& \Leftrightarrow x = {{1 – \sqrt 2 } \over {3 – \sqrt 2 }} = {{\left( {1 – \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)} \over {\left( {3 – \sqrt 2 } \right)\left( {3 + \sqrt 2 } \right)}} \cr 
& = {{3 + \sqrt 2 – 3\sqrt 2 – 2} \over {9 – 2}} = {{1 – 2\sqrt 2 } \over 7} \cr} \)

Câu 9 trang 62 Sách Bài Tập (SBT) Toán 9 Tập 1

Một hình  chữ nhật có kích thước là 25 cm và 40 cm . Người ta tang mỗi kích thước của hình chữ nhật thêm x cm. Gọi S và P thứ tự là diện tích và chu vi của hình chữ nhật mới tính theo x .

a)      Hỏi các đại lượng S và P có phải là hàm số bậc nhất của x không ? Vì sao ?

b)      Tính các giá trị tương ứng của P khi x nhận các giá trị ( tính theo đơn vị cm) sau :

0;          1;             1,5;          2,5;             3,5.

Gợi ý làm bài:

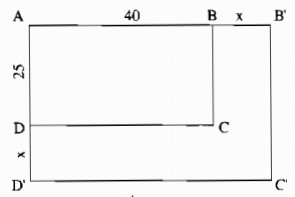
Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài

AB’= \(\left( {40 + x} \right)\)cm , chiều rộng B’C’= \(\left( {25 + x} \right)\) cm.

a) Diện tích hình chữ nhật mới :

\(S = \left( {40 + x} \right)\left( {25 + x} \right) = 1000 + 65x + {x^2}\)

S không phải là hàm số bậc nhất đồi với x vì có bậc của biến số x là bậc hai.

Chu vi hình chữ nhật mới:

\(P = 2.\left[ {\left( {40 + x} \right) + \left( {25 + x} \right)} \right] = 4x + 130\)

P là hàm số bậc nhất đối với x có hệ số a = 4 , hệ số b = 130.

b) Các giá trị tương ứng của P:

Trường Cao đẳng nghề Thừa Thiên Huế